弹簧质量阻尼系统方程解析与应用

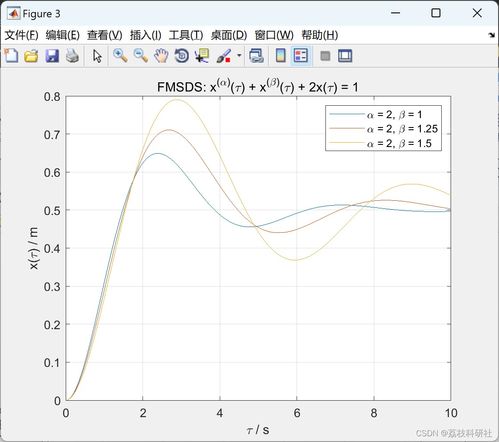
弹簧质量阻尼系统是力学中一个经典的模型，广泛应用于工程、物理学和机械设计等领域。本文将详细介绍弹簧质量阻尼系统的基本方程，并探讨其在实际应用中的重要性。

标签：弹簧质量阻尼系统，力学模型，基本方程

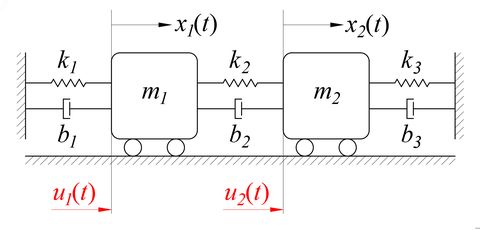
一、弹簧质量阻尼系统的基本组成

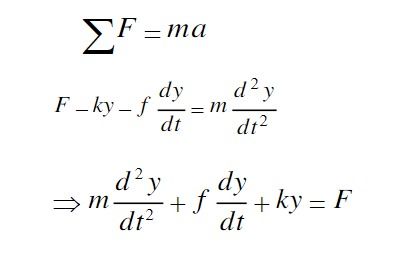
弹簧质量阻尼系统主要由质量块、弹簧和阻尼器三个部分组成。质量块代表系统中的物体，弹簧代表物体受到的弹性力，阻尼器代表物体受到的阻尼力。

标签：质量块，弹簧，阻尼器，系统组成

二、弹簧质量阻尼系统的运动方程

在弹簧质量阻尼系统中，物体的运动可以由牛顿第二定律来描述。设质量块的质量为m，弹簧的劲度系数为k，阻尼器的阻尼系数为c，物体的位移为x，速度为v，加速度为a，则系统的运动方程可以表示为：

[ mfrac{d^2x}{d^2} + cfrac{dx}{d} + kx = F() ]其中，F()为作用在质量块上的外力，通常为时间的函数。

标签：牛顿第二定律，运动方程，外力

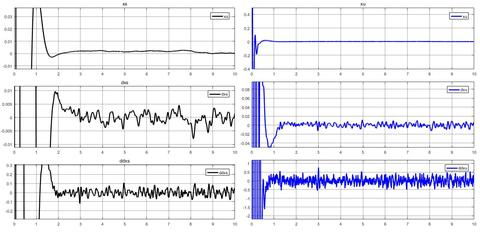
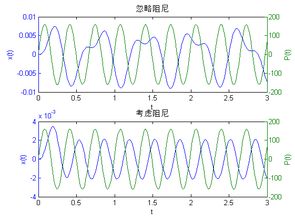
三、弹簧质量阻尼系统的解法

根据运动方程，我们可以求解系统的位移、速度和加速度随时间的变化。以下是几种常见的解法：

标签：解法，位移，速度，加速度

1. 零初始条件下的解法

当系统初始时刻的位移和速度均为零时，运动方程可以简化为：

[ mfrac{d^2x}{d^2} + cfrac{dx}{d} + kx = F() ]此时，我们可以通过求解二阶线性微分方程来得到系统的响应。

2. 非零初始条件下的解法

当系统初始时刻的位移和速度不为零时，运动方程可以表示为：

[ mfrac{d^2x}{d^2} + cfrac{dx}{d} + kx = F() ][ x(0) = x_0, quad v(0) = v_0 ]其中，( x_0 )和( v_0 )分别为初始位移和初始速度。此时，我们可以通过求解二阶线性微分方程的初值问题来得到系统的响应。

四、弹簧质量阻尼系统的应用

弹簧质量阻尼系统在工程和物理学中有着广泛的应用，以下列举几个实例：

标签：应用，工程，物理学

1. 振动控制

在机械结构设计中，弹簧质量阻尼系统可以用来控制振动，提高系统的稳定性和可靠性。例如，汽车悬挂系统、飞机起落架等。

2. 信号处理

在信号处理领域，弹簧质量阻尼系统可以用来模拟滤波器，实现信号的平滑和滤波。

3. 生物力学

在生物力学研究中，弹簧质量阻尼系统可以用来模拟人体关节的运动，分析人体运动过程中的力学特性。

五、总结

弹簧质量阻尼系统方程是力学中的一个基本模型，对于理解和分析系统的运动具有重要意义。本文详细介绍了弹簧质量阻尼系统的基本方程、解法及其应用，为相关领域的研究提供了参考。

标签：力学模型，应用